Problem :
What is the energy of a particle with mass 3.2×10-27 kilograms and velocity 0.9c?
E = γmc2 =  =
=  = 6.61×10-10
= 6.61×10-10 Joules.
Problem :
A particle has a momentum with magnitude 1.2×105 kgm/s and energy 4.42×10-11
Joules. What is its mass?
We know that
E2 + |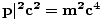
. The left hand side is equal to:
(4.42×10-11)2 + (1.2×105×3×108)2 = 1.30×1027 Therefore the mass is given by
m = 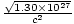 = 4.00×10-4
= 4.00×10-4 kilograms.
Problem :
Two protons approach each other from opposite direction, traveling with equal and opposite speeds 0.6c.
The collide to form a single particle that is at rest. What is the mass of this particle? (The proton mass is
1.67×10-27 kilograms).
We used a similar setup in Section 1 to show that
energy was conserved. There we saw
that conservation of momentum in a frame in which one of the protons was at rest gave:
M = 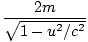 |
|
For the two protons this comes out as
4.175×10-27 kilograms. Clearly this is significantly more
than the sum of the masses.
Problem :
A particle of mass m and speed v approaches an identical particle at rest. The particles stick together
to form larger particle with mass M. What is the speed of the larger particle after the collision?
Conserving momentum in the frame of the particle at rest we have:
γvmv + 0 = γVMV,
where
V is the speed of the larger particle after the collision. Expanding this we have:
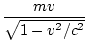 = =  |
|
Doing a little bit of algebra we find:
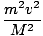 (1 - V2/c2) = V2(1 - v2/c2)âá’V = (1 - V2/c2) = V2(1 - v2/c2)âá’V = 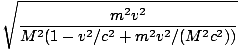 |
|
Problem :
Two particles with equal mass m approach each other with speed u. They collide to form a single
particle with mass M, which is at rest. Show the energy is conserved in the frame of the M particle.
We need to find an expression for
M. We followed through identical reasoning in
Heading
to show that:
M = 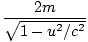 |
|
The expression for energy conservation in the rest frame of the large particle is:
γumc2 + γumc2 = (1)Mc2. We can cancel factor of
c2, substitute for
M and we find:
Hence the energy is the same after the collision as before in this frame.