Problem :
Find the inner product of the 4-momenta for the following two particles: a particle of mass m moving with
speed 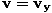 in the lab frame and a particle of mass M moving with velocity
in the lab frame and a particle of mass M moving with velocity  also
in the lab frame.
also
in the lab frame.
| Mmγvyγuy(c2 - vyuy) |
Problem : Calculate the same inner product as in the previous question, but now in a frame moving with one of the particles (or, if you already did it in such a frame, calculate it in the lab frame). Check that the result is the same.
In this frame the 4-momenta of the particle with speed vy is (mc, 0, 0, 0). The particle at rest in this frame sees the other particle moving in the y-direction with speed wy =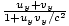 . Thus the 4-momentum is (γwyMc, 0, γwyMwy, 0). Thus the
inner product is:
. Thus the 4-momentum is (γwyMc, 0, γwyMwy, 0). Thus the
inner product is:
| Mmc2γwy |
But c2γwy is given by:
| c2γwy | = | 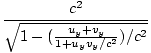 | |
| = | 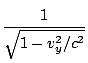  (c2 - uyvy) (c2 - uyvy) |
So the overall result is: Mmγvyγuy(c2 - uyvy), which is the same as above.
Problem : Prove that if A and B are 4-vectors, A.B their inner product is independent of the frame in which it is calculated.
The inner product in an arbitrary frame is given by:| A.BâÉáA0B0 - A1B1 - A2B2 - A3B3 |
Then using the definition of the 4-vector we have:
= 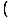 γ(A0' + vA1') γ(A0' + vA1')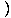 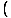 γ(B0' + vB1') γ(B0' + vB1')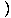 - - 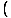 γ(A1' + vA0') γ(A1' + vA0')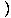 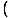 γ(B1' + vB0') γ(B1' + vB0') - A2'B2' - A3'B3' - A2'B2' - A3'B3' | |||
= γ2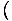 A0'B0' + v(A0'B0' + A1'B0') + v2A1'B1' A0'B0' + v(A0'B0' + A1'B0') + v2A1'B1' - γ2 - γ2 A1'B1' + v(A1'B0' + A0'B1') + v2A0'B0' A1'B1' + v(A1'B0' + A0'B1') + v2A0'B0' - A2'B2' - A3'B3' - A2'B2' - A3'B3' | |||
| = A0'B0'(γ2 - γ2v2) - A1'B1'(γ2 - γ2v2) - A2'B2' - A3'B3' | |||
| = A0'B0' - A1'B1' - A2'B2' - A3'B3' | |||
| âÉáA'.B' |
Which is the same as the inner product in some other inertial frame moving past with speed v.
Problem : Derive the velocity addition formula using the invariance of the 4-velocity inner product. In other words, if in frame A, B moves to the right with speed v, and C moves to the left with speed u, find w, the speed of B with respect to C.
First we must compute the 4-velocities of B and C in the frame of A. They are (γvc, γvv, 0, 0) for B and (γuc, - γuu) for C. Next, what are the 4-velocities of B and C in C's frame: for B (γwc, γww, 0, 0) and for C (c, 0, 0, 0). We can take the inner product of each of these pairs and set them equal since the inner product is frame invariant:
| (γvc, γvv, 0, 0).(γuc, - γuu, 0, 0) = (γwc, γw, 0, 0).(c, 0, 0, 0) | |||
| âá’γuγv(c2 + uv) = γwc2 | |||
âá’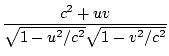 = =  |
Solving for w yields:
w = 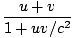 |
Which is the velocity addition formula.
Problem :
Again using the invariance of the inner product, determine the speed of one particle as observed by the other
as two particles approach each other with speed v along trajectories separated by an angle 2θ,
as shown in the figure below.

| (γvc, γvv cosθ, - γvv sinθ, 0).(γvc, γvv cosθ, γvv sinθ, 0) = (γwc, γww, 0, 0).(c, 0, 0, 0)âá’γv2(1 - v2cos 2θ) = γw |
where we used cos2θ - sin2θ = cos 2θ in the last equality. Expanding out for the γs, squaring, and solving for w yields:
w =  | |||
âá’w = 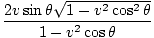 |













