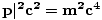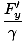sparknotes
Special Relativity: Dynamics
Terms and Formulae for Relativistic Dynamics
Terms
Relativistic energy
-
In Special Relativity the concept of total energy in the absence of a potential
E = 1/2mv
2
is replaced with another conserved
quantity
E = γmc
2
, where
m
is the mass or rest mass of the object. This quantity is conserved
in all collisions and decays. Where there is a potential involved it is the total energy
γmc
2 + V
which is conserved. Notice that an object at rest still has an amount of energy proportional to its mass
E
v=0 = mc
2
.
Relativistic momentum
-
The quantity that is conserved in all collisions in relativity is not
p = mv
but
p = γmv
. This is
called the relativistic momentum. When
v < < c
then
γ 
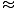1
and
p
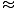mv
.
1
and
p
mv
.
4-vector
-
A vector with four components that, under a Lorentz transformation, transforms as
(cdt, dx, dy, dz)
does.
That is, for
A = (A
0, A
1, A
2, A
3)
the 4-vector in another frame must be:
Only those vectors for which the result of the above transformation is equal to the transformation of the individual coordinates under the Lorentz transformations are 4-vectors. The velocity 4-vector (γv, γbfv) and the energy-momentum 4-vector (E/c,
are the most common.
| A 0 = γ(A 0' + (v/c)A 1') | |||
| A 1 = γ(A 1' + (v/c)A 0') | |||
| A 2 = A 2' | |||
| A 3 = A 3' |
Only those vectors for which the result of the above transformation is equal to the transformation of the individual coordinates under the Lorentz transformations are 4-vectors. The velocity 4-vector (γv, γbfv) and the energy-momentum 4-vector (E/c,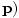
are the most common.
Proper time
-
The proper time interval between any two events is defined as:
This is a particularly useful quantity because it is in independent of the frame in which it is measured.
Δτ =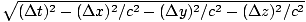 
|
This is a particularly useful quantity because it is in independent of the frame in which it is measured.
Inner product invariance
-
The inner product of two 4-vectors is defined as:
Note that the minus signs make this inner product different from the usual dot product in 3-space. When defined in this way, the inner product of any two 4-vectors is a constant, independent of frame (that is, it is independent of the frame in which the vectors are written).
| AƒB = A 0 B 0 - A 1 B 1 - A 2 B 2 - A 3 B 3 |
Note that the minus signs make this inner product different from the usual dot product in 3-space. When defined in this way, the inner product of any two 4-vectors is a constant, independent of frame (that is, it is independent of the frame in which the vectors are written).
Relativistic units
-
Are units in which
c
, the speed of light is given the value 1. This can be done in any number of ways;
setting the unit of distance equal to
3×108
meters is one way. Setting the unit of distance as
approximately 1 foot and the unit of time to 1 nanosecond also does the trick since the speed of light is
approximately 1 foot/nanosecond. This simplifies calculations immensely. If you need to find an exact
answer it is always possible to put the right number of factors of
c
back in at the end of a calculation by
looking at the units and working out where factors of m/s are missing.
Formulae
| Lorentz Transformations for Energy and Momentum |
|
| Formula for Velocity in terms of Energy and Momentum |
|
= 
| Relativistic relationship between mass, energy, and momentum. (Specifically, this equation states that the square of the energy-momentum 4-vector is equal to m 2 c 4 .) The formula reduces to the familiar E = mc 2 when the momentum p is zero. |
|
| Lorentz transformations for force undergoing a boost in the y-direction. |
|
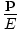Become a fan on Facebook
Follow us on Twitter
