Problem :
Suppose we have a system of 3 particles, each of which can be in one of
three states, A, B, and C, with equal probability. Write an
expression that represents all of the possible configurations of the
entire system, and determine which configuration will be most likely
(such as "2 particles in state A, one in state B").
(A + B + C)3 = A3 + B3 + C3 +3A2B + 3A2C + 3B2A + 3B2C + 3C2A + 3C2B + 6ABC
The unexpanded (A + B + C)3 represents all of the possible configurations
of the system. Most probable is the configuration in which one particle
is in each state, above represented in the expansion by 6ABC, with a
probability of  .
.
Problem :
Return to the binary system discussed before. If the system consists of
5 particles, how many states of the entire system have 3 magnets in the
up position?
Here, we only need to plug in N = 5 and U = 3 into our equation for
g(N, U).
g(5, 3) =
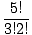
= 10
Problem :
Take a system with 20 possible states, all equally likely. What is the
probability of being in any particular state?
A simple problem, given our probability equation. P = 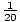 = 0.05.
= 0.05.
Problem :
In certain quantum scenarios, there are two distinct energy levels that
a particle may occupy. Let one of the levels have an energy U which
is equal to U1 = 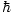 σ, and let the other level have energy
U2 = 2
σ, and let the other level have energy
U2 = 2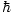 σ. Let us further suppose that the particle is twice
as likely to be in level 1 than in level 2. What is the average value
of the energy?
σ. Let us further suppose that the particle is twice
as likely to be in level 1 than in level 2. What is the average value
of the energy?
We need to use the equation for average value of a property:
<
U > =
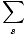 U
U(
s)
P(
s) =

 σ
σ +
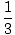
2
 σ
σ =
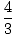
 σ
σ
Problem :
State the Fundamental Assumption, and explain how it is related to the
function P(s).
The Fundamental Assumption states that any closed system has an equal
probability to be in any of its possible quantum states. Using this, we
showed that P(s) is given simply by 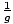 for g possible
states.
for g possible
states.