Problem :
We can define the spin of any collection of particles to be the sum of
the spins of the individual particles that comprise it. Given that
protons and electrons are of spin 1/2, specify whether the hydrogen atom
is a fermion or a boson.
The Hydrogen atom consists of an electron and a proton, so the total
spin is 1. Therefore, the Hydrogen atom is a boson.
Problem :
What is the energy of one mole of an ideal gas at room temperature?
This problem tests whether you remember all of the conversions between
fundamental and conventional units, and tests whether you can recall the
equation we derived for the energy of an ideal gas. Recall that
U = 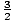 Nτ. N here will be Avogadro's Number, which is
6.02×1023. Room temperature is 25oC, which is
298K. Therefore τ = 298kB. The final result gives us U = 2477
Joules.
Nτ. N here will be Avogadro's Number, which is
6.02×1023. Room temperature is 25oC, which is
298K. Therefore τ = 298kB. The final result gives us U = 2477
Joules.
Problem :
Give the two heat capacities for a mole of ideal gas.
We recall that CV = 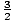 N and Cp =
N and Cp = 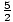 N. Therefore,
CV = 9.03×1023 and Cp = 1.51×1024.
N. Therefore,
CV = 9.03×1023 and Cp = 1.51×1024.