Particle Physics Background
Before we talk about gases, we need to understand a few more results
from quantum mechanics. We will sometimes use the word "orbital" here
to mean a state possible for one particle.
Every fundamental particle is of one of two types. A fermion is a
particle with half-integer spin. For example, an electron has a spin of
1/2. A boson is a particle with integer spin. For example, a
photon is a boson because it has spin 1.
The difference in the two types of particles can be characterized by what
is known as the "Pauli Exclusion Principle", which insists that an orbital
can only be occupied by 0 or 1 fermions. Bosons, on the other hand, can be
fit without limit into a single orbital. This fact alone leads to radically
different behavior under certain conditions, such as low temperature.
Classical Distribution Function
There is a bit of convention that must be established now. Instead of
writing < N(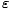
) > for the average number of particles in a
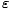particular orbital of energy , we write f ().
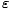f is known as the distribution function, and its value is of
course dependent on the type of system that we are talking about.
Notice that the difference between fermions and bosons has to do with
orbitals having an occupancy N larger than 1. For this reason, we
presume that fermions and bosons behave similarly for sparsely populated
orbitals; that is, for f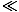
1. We call this condition the classical
regime, because it doesn't depend on the quantum distinctions between
particles.
It has been known for quite some time that the classical distribution
function is given by:
Ad-free experience
Study Guides for 1,000+ titles
Full Text content for 250+ titles
No Fear Translations of Shakespeare’s plays (along with audio!) and other classic works
Flashcards
Mastery Quizzes
Infographics
Graphic Novels
AP® Practice & Lessons
Note-taking
Bookmarking
Dashboard
