Thermodynamics: Gas

Topics

Non-Classical Gases

Save

Topics Non-Classical Gases

Fermi Gas

A Fermi gas is a gas consisting of fermions. We will investigate a few of its properties and applications here.

Fermi-Dirac Distribution Function

Consider a system that is a single orbital for a fermion. Remember that only 0 or 1 fermions may be in the orbital. The Gibbs sum is easy to calculate then; in fact, we already solved this problem in a previous problem set: Z_G = 1 + λe^-/τ. We can then directly calculate f, remembering that it is equivalent to < N >.

f (

) =

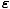
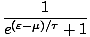
Notice that in the classical limit, f must be much less than 1, so the exponential must be large compared to one. An expansion yields the classical distribution function we derived before.

Fermi Level

We are concerned with the case where the gas is dense compared to the quantum concentration. The gas is called degenerate in this regime, as opposed to in the classical regime already discussed.

The chemical potential in general is a function of the temperature. However, we define the chemical potential at a temperature of zero for a fermi gas to be μ(τ = 0) = 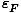where 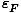is called the Fermi energy.

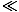
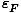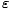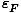The significance of the Fermi energy is that for τ, the orbitals of energy ≤ are completely occupied and the orbitals above the Fermi energy are completely vacant.