Did you know you can highlight text to take a note? x

Calculating the pH of Strong Acid and Strong Base Solutions

When a strong acid or a strong base is added to water, it nearly completely dissociates into its ion constituents because it has a pKa or pKb less than zero. For example, a solution of H2SO4 in water contains mostly H+ and SO42-, and almost no H2SO4 is left undissolved. This makes calculating the pH of a strong acid or strong base solution exceedingly simple--the concentration of acid equals the concentration of H+. Recall that pH is computed by taking the negative log of of [H+]. Common strong acids that should be memorized include HCl (hydrochloric), HNO3 (nitric), HClO4 (perchloric), and H2SO4 (sulfuric). Strong bases include Group I hydroxides (LiOH, NaOH, KOH, etc.) and Group II hydroxides except for Be(OH)2 and Ba(OH)2.

Calculating the pH of Weak Acid and Weak Base Solutions

Calculating the pH of weak acid and weak base solutions is much more complicated than the above case--weak acids and bases do not completely dissociate in aqueous solution but are in equilibrium with their dissociated forms. Therefore, we must apply what we know about equilibria to solve these types of problems. For example, let's calculate the pH of a 0.10 M solution of acetic acid in water. To do this, we first write down the equilibrium involved and the expression for the equilibrium constant:

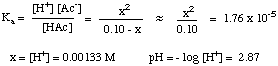
Figure %: Note that H+ represents H3O+ in the equilibrium constant expression.

Next, you should compile a table of values for the concentration of all species involved in the equilibrium. We already know that the initial concentration, [ ]o, of acetic acid is 0.10 M and that the initial concentration of H+ is 10-7 (since the solvent is neutral water). Even though there is an initial concentration of H+ in solution, it is so small compared to the amount produced by the acid that it is usually ignored. From the stoichiometry of the reaction, one mole of H+ and one mole of acetate (Ac-) are produced for each mole of acetic acid dissociated. Therefore, if we denote the amount of acetic acid dissociated as x, the final concentrations of H+ and Ac- are both x, and the final concentration of HAc in solution is 0.10 M - x. This data is summarized in :

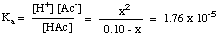
Figure %: Table of equilibrium values for the dissociation of acetic acid

After you have compiled the table of values, you can substitute the equilibrium concentration values for each species into your expression for Ka as shown below:

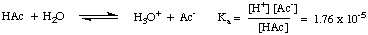
You should note that the above equation is a quadratic equation in x and therefore requires use of the quadratic equation to solve for x. If, however, we can make the assumption that [HAc]o - x = [HAc]o, the equation becomes much easier to solve. We can do this if HAc is a weak enough acid that it dissociates very little, and the change in [HAc] is negligible.

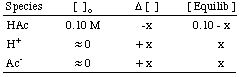
Is this assumption valid? Solving the quadratic equation using the quadratic formula gives a pH of 2.88. The difference of 0.01 pH unit is small enough to be insignificant, so the assumption is valid in this case and will certainly save you some time on a test. We can make the approximation [HA]o - x = [HA]o so long as x is less than 5% of the initial concentration of HA. X will be greater than 5% of [HA]o with stronger weak acids at low concentrations. Consider these guidelines when you decide whether or not to make the approximation: you can simplify the quadratic equation if the solution is more concentrated than 0.01 M and the pKa of the acid is greater than 3.

Previous section Next page The pH of Non-Buffered Solutions page 2

Take a Study Break