Things cost more today than they used to. In the 1920's, a loaf of bread cost about a nickel. Today, it costs more than $2. In general, in the United States the overall level of prices rises from year to year. This phenomenon of rising prices is called inflation.
While small changes in the price level from year to year may not be that noticeable, these small changes add up over time, leading to big effects. From 1924 to 2024, the average rate of inflation in the United States from year to year has been just under 3 percent. This small year-to-year inflation level led to an 18-fold increase in overall cost of living during that same period.
Inflation plays an important role in the macroeconomic economy by changing the value of a dollar over time. This section on inflation will explain how to calculate inflation, first using the CPI and then using a second measure, the GDP deflator.
Calculating Inflation Using the CPI
The price level index most commonly used in the United States is the CPI, or consumer price index. Thus, the simplest and most common method of calculating inflation is to calculate the percentage change in the CPI from one year to the next. In the example of Country B in the previous section, the price level increased from 100 in time period 1 (the base period) to 141 in period 2. The percent change in the price level from the base period to the comparison period is calculated by subtracting 100 from the comparison CPI. In this example, the percent change in the price level is \(141 - 100 = 41\%\).
If the time periods are years, then from period 1 to period 2, Country B experienced an annual inflation rate of 41 percent. (For a real country, this would be big red flag. In healthy economies, annual inflation as a percentage rarely hits double digits.)
While it is simple to calculate the inflation rate between the base period and a comparison period, it is a bit more difficult to calculate the rate of inflation between two comparison periods. To make this calculation, first check that both comparison periods use the same base period. Next, to calculate the percentage change in the level of the CPI, subtract the CPI for the later period from the CPI for the earlier period, and then divide by the CPI for the earlier period.
In the example of Country B, the CPI for period 2 was 141 and the CPI for period 3 was 182. Since the base period for these CPI calculations was period 1, we must use the method of calculating inflation between two comparison periods. We need to subtract the CPI for the later period from the CPI for the earlier period and then divide by the CPI for the earlier period. That gives \((182−141)/141 = 0.29 = 29\%\). Thus, the rate of inflation from period 2 to period 3 was 29% per period.
Notice that this method also works for calculating the rate of inflation between a base period and a comparison period. For instance, the CPI for period 1 was 100, and the CPI for period 2 was 141. Using the formula above gives \((141−100)/100= 0.41 = 41\%\).
Calculating Inflation Using the GDP Deflator
The other major price index used to determine the price level is the GDP deflator, which measures how much of the change in the GDP from a base year is a function of changes in the price level. The GDP deflator is calculated by dividing the nominal GDP by the real GDP and multiplying by 100:
\(\text{GDP Deflator} = (\text{Nominal GDP}/\text{Real GDP}) \times 100\)
Let's stick with imaginary Country B, and now suppose that its prices and total output are as shown in the next table.
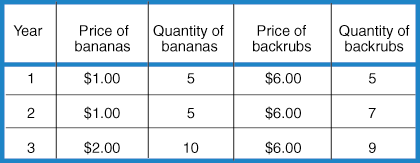
We will calculate the GDP deflator for year 3, using year 1 as the base year. To do this, we first must determine both nominal GDP and real GDP in year 3. Nominal GDP in year 3 is \((10×$2)+(9×$6) = $74\), and real GDP in year 3 using year 1 as the base year (so, year 3 output measured in year 1 prices) is \((10×$1)+(9×$6) = $64\).
Therefore, the GDP deflator for year 3 is \(($74/$64)×100=116\).
If we were to use the same method to calculate the GDP deflator for years 1 and 2, both times using year 1 as the reference year, we would get \(($35/$35)×100=100\) for year 1 and \(($47/$47)×100=100\) for year 2. The value for 100 for year 1 is to expected, because year 1 is the reference year. The value of 100 for year 2 might be surprising, until we look at the table and notice that prices did not change at all from year 1 to year 2. The GDP increase from $35 to $47 was entirely due to a rise in productivity.
What about inflation? It was zero between years 1 and 2 (no change in prices), but between year 2 and 3 there was an increase in the GDP deflator of \((116−100)/100 = 0.16=16\%\). Using the GDP as the inflation measure gives us an annual inflation rate of 16 percent.
Pros and Cons of the CPI and the GDP Deflator
The CPI uses a fixed basket of goods. The GDP deflator, in essence, takes the entire (final) output of the economy as its “basket” and allows the contents of the basket to vary from year to year. The inflation rates calculated from the CPI and GDP deflator are usually fairly similar in value. However, both inflation measures are biased.
The CPI, as already discussed, doesn’t account for substitution and the introduction of new items. The GDP deflator, by contrast, automatically and fully accounts for substitution and the introduction of new items, but doesn’t account for the effect on consumers who have to adjust their buying habits. To illustrate this point, imagine that a livestock disease kills all of a country’s beef cattle. As a result, people will buy much less beef (all of it imported) and purchase a lot more chicken instead. The GDP deflator will record this change just as the same as if people’s tastes had suddenly changed. But in reality, people were forced to make the change. Their earlier buying habits suggest that some of them, at least, like chicken less than beef, but now they have to eat beef. Relative to what they prefer, their purchasing power went down, because a good the consumers were willingly buying was taken away. In general, if the CPI tends to overestimate the impact of price increases on households’ purchasing power, the GDP deflator tends to underestimate the impact.













