Previous Next

To simplify an expression with exponents, first simplify each term according to multiplication, division, distribution, and power to power rules. Then, combine like terms and arrange the terms, putting those with variables first, in order of highest exponent. Sometimes like terms are only evident when one rewrites some of the terms using the "power of a power" rule.

Example 1: Simplify (5x)2 + (x3)2 + (5x)(2x3).

(5x)2 + (x3)2 + (5x)(2x3)
= 52x2 + x3(2) + (5)(2)x1+3
= 25x2 + x6 +10x4
= x6 +10x4 +25x2

Example 2: Simplify 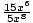+ (x3)7 -2x2 +2x3.

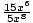+ (x3)7 -2x2 +2x3
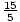= x6-8 + x3(7) -2x2 +2x3
= 5x-2 + x21 - 2x2 +2x3
= x21 + 2x3 -2x2 +5x-2

Example 3: Simplify 2x2 +6x3 -3x3 + (4xy)2 + (5 + x)3 -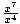

2x2 +6x3 -3x3 + (4xy)2 + (5 + x)3 -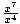
= 2x2 +3x3 +42x2y2 + (5 + x)3 - x3
= 16x2y2 + (5 + x)3 +2x3 +2x2

Example 4: Simplify (x2 +2x2)5 - (3x3)(4x4) + (11x)2

(x2 +2x2)5 - (3x3)(4x4) + (11x)2
= (3x2)5 - (3)(4)x3+4 +112x2
= 35x2(5) -12x7 +121x2
= 243x10 - 12x7 +121x2

Example 5: Simplify (x + 3)5 + x5x4x3 -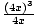

(x + 3)5 + x5x4x3 -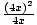
= (x + 3)5 + x5+4+3 - (4x)3-1
= (x + 3)5 + x12 - (4x)2
= (x + 3)5 + x12 - 42x2
= (x + 3)5 + x12 - 16x2
= x12 + (x + 3)5 -16x2

Previous section Next section

Take a Study Break