Imaginary Numbers
Until now, we have been dealing with real
numbers. We have not been able
to take the square root of a negative number because the square root of a
negative number is not a real number. Instead, the square root of a negative
number is an imaginary number--a number of the form 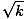 , where k < 0. Imaginary numbers are represented as ki, where i =
, where k < 0. Imaginary numbers are represented as ki, where i =  . For
example,
. For
example, 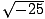 = 5i and
= 5i and  = i
= i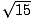 .
.
We can simplify square roots of negative numbers by factoring out  = i and simplifying the resulting root.
= i and simplifying the resulting root.
Examples:
- Simplify
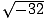 .
.
- Simplify
 .
.
- Simplify
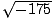 .
.
Observe the following:
| i1 | = | i |
|
| i2 | = | (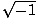 )2 = - 1 )2 = - 1 |
|
| i3 | = | i2i = - 1(i) = - i |
|
| i4 | = | i3i = - i(i) = - i2 = - (- 1) = 1 |
|
| i5 | = | i4i = 1(i) = i |
|
| i6 | = | i5i = - 1 |
|
| i7 | = | i6i = - i |
|
| i8 | = | i7i = 1 |
|
| i9 | = | i |
|
| | ... | |
|
Thus, we can find
in using the following:
- If n÷4 leaves a remainder of 1, in = i.
- If n÷4 leaves a remainder of 2, in = - 1.
- If n÷4 leaves a remainder of 3, in = - i.
- If n÷4 leaves no remainder, in = 1.
Examples:
- What is i54?
54÷4 = 13R2.
Thus, i54 = - 1.
- What is i103?
103÷4 = 25R3.
Thus, i103 = - i.