Previous Next


Examples:

4(2 + 5i) = 4(2) + 4(5i) = 8 + 20i
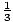(6 - 9i) = 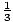(6) + 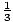(- 9i) = 2 - 3i.
-2(11 - 2i) = - 2(11) + (- 2)(- 2i) = - 22 + 4i.
2i(5 + 7i) = 2i(5) + 2i(7i) = 10i + 14i2 = 10i + 14(- 1) = - 14 + 10i.

Multiplying Complex Numbers

To multiply two complex numbers, use the FOIL method and treat each complex number as an ordinary binomial. Then simplify the i2 term (i2 = - 1) and combine like terms.


(a1 + b1i)(a2 + b2i)=a1a2 + a1b2i + a2b1i + b1b2i2  
 =a1a2 + (a1b2 + a2b1)i + b1b2(- 1)  
 =(a1a2 - b1b2) + (a1b2 + a2b1)i.  


Examples:

(2 + 3i)(5 + 2i) = ?


 =10 + 4i + 15i + 6i2  
 =10 + 19i - 6  
 =4 + 19i.  

(3 - 4i)(6 + i) = ?


 =18 + 3i - 24i - 4i2  
 =18 - 21i + 4  
 =22 - 21i.  

(7 - 2i)(6 - 2i) = ?


 =42 - 14i - 12i + 4i2  
 =42 - 26i - 4  
 =38 - 26i.  

(2 + 3i)2 =?


 =(2 + 3i)(2 + 3i)  
 =4 + 6i + 6i + 9i2  
 =4 + 12i - 9  
 =-5 + 12i.  

(5 + 4i)(5 - 4i) = ?


 =25 - 16i2  
 =25 + 16  
 =41.  

Previous page Complex Numbers page 1 Next section

Take a Study Break