Discrete Functions

Topics

The Factorial Function

Save

Topics The Factorial Function

Occasionally, we will encounter a situation in which the choices are not distinct. For example, in how many ways can he letters of the word ALGEBRA be arranged?

Since an arrangement with the first A in the 5^th spot and the last A in the 6^th spot is no different than an arrangement with the first A in the 6^th spot and the last A in the 5^th spot, we must account for the overlap. The total number of possibilities is = = 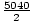2520. We divide by 2! because n! is the number of ways n A's can be arranged.

To find the total number of possibilities when choices are not distinct, divide by the factorial of the number of choices that are the same. If 2 choices are the same as each other, and 2 different choices are the same as each other, divide by 2!2!. If 2 choices are the same as each other, and 3 different choices are the same as each other, divide by 2!3!.

Example 3: In how many ways can the letters of the word BANANA be arranged?

There are 6 letters, 3 A's, and 2 N's. Thus, the letters can be arranged in 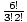= = 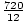60 different ways.