Previous Next

Recursively Defined Functions

Most of the functions we have dealt with in previous chapters have been defined explicitly: by a formula in terms of the variable. We can also define functions recursively: in terms of the same function of a smaller variable. In this way, a recursive function "builds" on itself.

A recursive definition has two parts:

  1. Definition of the smallest argument (usually f (0) or f (1)).
  2. Definition of f (n), given f (n - 1), f (n - 2), etc.

Here is an example of a recursively defined function:


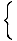
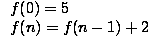
We can calculate the values of this function:


f (0)=5  
f (1)=f (0) + 2 = 5 + 2 = 7  
f (2)=f (1) + 2 = 7 + 2 = 9  
f (3)=f (2) + 2 = 9 + 2 = 11  
…    

This recursively defined function is equivalent to the explicitly defined function f (n) = 2n + 5. However, the recursive function is defined only for nonnegative integers.

Here is another example of a recursively defined function:


The values of this function are:


f (0)=0  
f (1)=f (0) + (2)(1) - 1 = 0 + 2 - 1 = 1  
f (2)=f (1) + (2)(2) - 1 = 1 + 4 - 1 = 4  
f (3)=f (2) + (2)(3) - 1 = 4 + 6 - 1 = 9  
f (4)=f (3) + (2)(4) - 1 = 9 + 8 - 1 = 16  
…    

This recursively defined function is equivalent to the explicitly defined function f (n) = n2. Again, the recursive function is defined only for nonnegative integers.

Here is one more example of a recursively defined function:

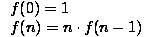
The values of this function are:


f (0)=1  
f (1)=1ƒf (0) = 1ƒ1 = 1  
f (2)=2ƒf (1) = 2ƒ1 = 2  
f (3)=3ƒf (2) = 3ƒ2 = 6  
f (4)=4ƒf (3) = 4ƒ6 = 24  
f (5)=5ƒf (4) = 5ƒ24 = 120  
…    

This is the recursive definition of the factorial function, F(n) = n!.

Not all recursively defined functions have an explicit definition.

Previous section Next page Recursively Defined Functions page 2

Take a Study Break