Previous Next

The solutions to y = f (x) when y = 0 are called the roots of a function (f (x) is any function). These are the points at which the graph of an equation crosses the x-axis.

Roots of Quadratic Functions

We have already learned to solve for x in ax2 + bx + c = 0 by factoring ax2 + bx + c and using the zero product property. Since the roots of a function are the points at which y = 0, we can find the roots of y = ax2 + bx + c = 0 by factoring ax2 + bx + c = 0 and solving for x. We can also find the roots of y = ax2 + bx + c = 0 using the quadratic formula, and we can find the number of roots using the discriminant.

If a quadratic function has 2 roots--i.e., if it can be factored into 2 distinct binomials or if b2 -4ac > 0--then it crosses the x- axis twice. Either the vertex is below the x-axis and the leading coefficient is positive, or the vertex is above the x-axis and the leading coefficient is negative.

If a quadratic function has 1 root (a "double root")--i.e. if it can be factored as the square of a single binomial or if b2 - 4ac = 0--then it crosses the x-axis once. The vertex lies on the x-axis, and the leading coefficient can be positive or negative.

If a quadratic function has no roots--i.e. if it cannot be factored or if b2 -4ac < 0--then it does not cross the x-axis. Either the vertex is above the x-axis and the leading coefficient is positive, or the vertex is below the x-axis and the leading coefficient is negative. The quadratic equation is said to have 2 imaginary roots.

Roots of Other Polynomial Functions

We can find the roots of other polynomial functions by setting y = 0 and factoring. For example, y = x3 -27 = (x - 3)(x2 +3x2 + 9) has one root (x = 3), because there is one value of x for which x - 3 = 0 and no values of x for which x2 + 3x + 9 = 0 (the discriminant is negative). y = 45x3 +18x2 - 5x - 2 = (3x + 1)(3x - 1)(5x + 2) has three roots (x = - ,, - ).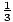

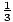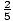Previous section Next page Roots page 2

Take a Study Break