Previous Next

Problem : Find the inverse of f (x) = .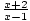

y =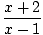    

Solve for x first:


(x - 1)y = x + 2  
xy - y = x + 2  
xy - x = y + 2  
x =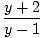  

Now switch the variables x and y:

y =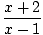    

Problem : Find the inverse of f (x) = 6 + 5x3.


y = 6 + 5x3  
x =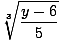  

Now switch variables:

y =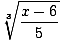    

Problem : If f (3) = 2 and f'(3) = 7, what is (f-1)'(2)?

(f-1)(2) = , since the slope of the inverse is the reciprocal.

Problem : Find (f-1)'(2) for f (x) = 4x3 - 2x + 2.

Note that f is not one-to-one throughout its domain, so it does not have an inverse defined on its entire range. However, there is a unique x, namely 0, such that f (x) = 2. So, for a suitable domain containing 0, the inverse can be defined, and we may compute:


(f-1)'(2) =  
  =  
  = -  

Problem : Find (f-1)'(- 4) for f (x) = x3 - x2 - 4x.

This problem doesn't make much sense, since there are several x's such that f (x) = - 4. Namely, they are x = - 2, 1, or 2.
Previous section Next section

Take a Study Break