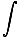 axdx= axdx=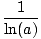 ax+c ax+c |
|
Derivatives of Logarithms
It may be satisfying to learn now that for x>0,
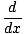 ln(x) = ln(x) =  |
|
The appeal rests in the corresponding implication that
Recall that the power rule did not offer a way of integrating the function 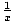 ,
but now it is possible to do so.
,
but now it is possible to do so.
A related rule for logarithms of any base is that
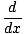 loga(x) = loga(x) = 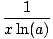 |
|
Logarithmic Differentiation
To find the derivative of a constant raised to a power of x, the rule presented earlier in
this section should suffice. However, to find the derivative of a function of x that is
raised to a power of x, the technique of logarithmic differentiation is necessary.
Example: Differentiate y = x3x.
Step One: Take the natural log of both sides of the equation:
ln(y) = ln(x3x).
Step Two: Now use log rules to take the variable x out of the exponent and
turn it into a product: ln(y) = (3x)(ln(x)).
Step Three: Implicitly differentiate both sides with respect to x (remember to use the
chain rule):
Step Four: Solve for 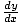 algebraically:
algebraically:
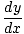 | | = 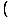 3+3 ln(x) 3+3 ln(x)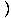 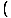 y y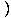 |
|
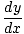 | | = 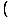 3+3 ln(x) 3+3 ln(x)  x3x x3x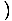 |
|
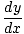 | | = 3x3x +3x3xln(x) |
|