This final unit in the study of calculus AB begins with a discussion of inverse functions and the algebraic and geometric relationship between a function f and its inverse f-1. The geometric property of f-1 as a reflection of f across the line y = x is used to develop a formula for finding the derivative of f-1 from f.

Next is an introduction to the function f (x) = ex and its inverse f (x) = ln(x). After a brief discussion of the properties of these functions, we see that the derivative of f (x) = ex is in fact ex itself, and that the derivative of f (x) = ln(x) is the function 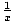, which is the only power function that could not be integrated by reversing the power rule. The derivatives of ex and ln(x) are used to develop methods to differentiate functions where x is in the exponent. Finally, the general form of functions that exhibit exponential growth or decay is presented.

Next section

Take a Study Break