In studying polynomial functions, it is
therefore enough to find the derivative of a monomial function of the form
f (x) = axn. Plugging into the formula for the derivative, we have
| f'(x) | = | 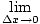 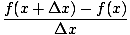 |
|
| | = | 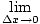 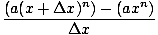 |
|
| | = | 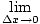 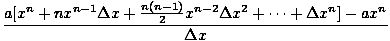 |
|
| | = | 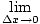 a[nxn-1 + a[nxn-1 +  xn-2Δx + ... + Δxn-1] xn-2Δx + ... + Δxn-1] |
|
| | = | anxn-1 |
|
Thus, to take the derivative of a monomial function, we multiply by the exponent and
reduce the exponent by 1. Using the property of the derivative mentioned above, we
see that the derivative of the polynomial function f (x) = anxn + ... + a1x + a0 is
given by f (x) = nanxn-1 + ... + a2x + a1.
We will wait until we have the quotient rule at our disposal before we calculate the
derivatives of rational functions.
Derivatives of Power Functions
A power function has the form
f (t) = Crt. Plugging into the formula for the derivative, we have
The limit in the final expression above does not depend on t, so it is a
constant. In fact, this limit is one way of defining the value of the natural
logarithm function at r, or log(r). Thus we have
In the special case where r = e, where e is the number such that log(e) = 1, we
have f'(t)=f(t). The functions f (t) = Cet are the only functions
that are equal to their own derivatives.