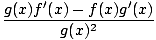-
Natural Logarithm
There is a unique positive number e such that the function f (t) = et is its own derivative. The natural logarithm of a positive real number x is the logarithm of x with base e, denoted log(x). Alternately,
log(x) =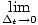 
-
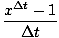
Chain Rule
The formula for the derivative of a composition of functions. If h(x) = fog(x) = f (g(x), then:
h'(x) = f'(g(x))g'(x).
-
Implicit Differentiation
A method for differentiating implicit functions, without necessarily solving for them, by differentiating the terms of the defining equation.
-
Product Rule
The formula for the derivative of a product of functions:
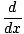[f (x)g(x)] = f (x)g'(x) + g(x)f'(x)
-
Quotient Rule
The formula for the derivative of a quotient of functions (which is a consequence of the product rule). If q(x) = f (x)/g(x), then:
q'(x) = 
