Problem :
Compute U3(f, 0, 3) and L3(f, 0, 3) for f (x) = (x - 2)2.
We subdivide the interval
[0, 3] into the three intervals
[0, 1],
[1, 2],
[2, 3], so that
M1 = f (0) = 4,
M2 = f (1) = 1,
M3 = f (3) = 1, and
m1 = f (1) = 1,
m2 = f (2) = 0,
m3 = f (2) = 0. Therefore,
| U3(f, 0, 3) | | =  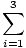 Mi = Mi =  (4 + 1 + 1) = 2 (4 + 1 + 1) = 2 |
|
| L3(f, 0, 3) | | =  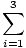 mi = mi =  (1 + 0 + 0) = (1 + 0 + 0) =  |
|
We may conclude that
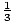 ≤
≤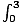 (x - 2)2dx≤2
(x - 2)2dx≤2.
Problem :
Compute 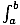 - 1dx.
- 1dx.
This definite integral is equal to the area of a rectangle with height
1 unit and
length
(b - a) units lying below the
x-axis. The area therefore counts as
negative, so the definite integral equals
- (1)(b - a) = a - b.