Previous

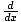
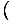
Problem : Find f (t)dt.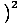

It follows from the chain rule and the fundamental theorem of calculus that

f (t)dt = 2f (t)dtf (x)    

Problem : Find all antiderivatives of f (x) = 1/(1 + x) + 2 cos(2x).

We guess the antiderivative

F(x) = log(1 + x) + sin(2x)    

and check that F'(x) = f (x). All other antiderivatives must be of the form F(x) + c for some constant c.

Problem : Compute 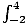(3x2 + 7)dx using the fundamental theorem of calculus.

We choose x3 + 7x as an antiderivative of 3x2 + 7. The fundamental theorem of calculus then gives


3x2 + 7dx=x3 +7x|-24  
 =(43 +7(4)) - ((- 2)3 + 7(- 2))  
 =114  

Previous section

Take a Study Break