Previous Next

Problem : Calculate the derivative of f (x) = x2 at x = 1.

Substituting 1 for x0 in the formula for the derivative, we have


f'(1)=  
 =  
 =2 + Δx  
 =2  

Observing the graph of f (x) = x2, we see that this is the slope of the tangent to the graph at the point (1, f (1)) = (1, 1).

Problem : Find the vertex of the parabola f (x) = x2 + 2x + 2 using the derivative.

At the vertex, the tangent line to the graph will be horizontal, with slope 0. Therefore, we search for an x such that f'(x) = 0. We have


f'(x)=limΔx→0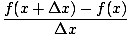  
 =limΔx→0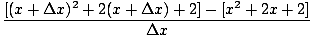  
 =limΔx→0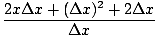  
 =limΔx→02x + 2 + Δx  
 =2(x + 1)  

Thus f'(x) = 0 if and only if x = - 1. Now f (x) = (- 1)2 + 2(- 1) + 2 = 1, so the vertex of the parabola is (- 1, 1). We can check this by noting that f (x) - 1 = (x + 1)2, so the graph of f (x) is the graph of x2 translated 1 unit to the left and 1 unit up.

Problem : Find the equation of the tangent line to the graph of f (x) = x3 at x = 2.

First we compute f'(2):


f'(2)=limΔx→0  
 =limΔx→0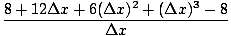  
 =12  

The equation of the line through (2, f (2)) = (2, 8) with slope 12 is given by y = 12(x - 2) + 8.
Previous section Next section

Take a Study Break