Problem :
Compute  x sin(x)dx.
x sin(x)dx.
Letting
f (x) = x and
g(x) = sin(x) in the formula for integration by parts, we have
 x sin(x)dx x sin(x)dx | = | - x cos(x) -  (- cos(x))dx (- cos(x))dx |
|
| | = | - x cos(x) + sin(x) + C |
|
Problem :
Find  x2exdx.
x2exdx.
Letting
f (x) = x2 and
g(x) = ex, we have
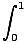 x2exdx x2exdx | = | x2ex|01 = 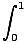 2xexdx 2xexdx |
|
| | = | e - 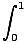 2xexdx 2xexdx |
|
Applying integration by parts again, we get
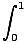 2xexdx 2xexdx | = | 2xex|01 - 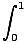 2exdx 2exdx |
|
| | = | 2e - (2ex|01) |
|
| | = | 2 |
|
Substituting the value of this integral back in the first computation yields
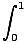 x2exdx = e - 2 x2exdx = e - 2 |
|
Problem :
Express  sinn+2(x)dx in terms of
sinn+2(x)dx in terms of  sinn(x)dx by
integrating by parts twice.
sinn(x)dx by
integrating by parts twice.
Let
I =  sinn+2(x)dx
sinn+2(x)dx, the integral we are trying to compute.
Integrating by parts gives
 sinn+2(x)dx sinn+2(x)dx | = |  sinn+1(x)sin(x)dx sinn+1(x)sin(x)dx |
|
| | = | sinn+1(x)(- cos(x)) -  (n + 1)sinn(x)cos(x)(- cos(x))dx (n + 1)sinn(x)cos(x)(- cos(x))dx |
|
| | = | -sinn+1(x)cos(x) + (n + 1) sinn(x)cos2(x)dx sinn(x)cos2(x)dx |
|
Integrating this new integral by parts, we have
 sinn(x)cos2(x)dx sinn(x)cos2(x)dx | = |  sinn(x)(1 - sin2(x))dx sinn(x)(1 - sin2(x))dx |
|
| | | =  sinn(x)dx - sinn(x)dx -  sinn+2(x)dx sinn+2(x)dx |
|
| | | =  sinn(x)dx - I sinn(x)dx - I |
|
Thus
I = - sinn+1(x)cos(x) + (n + 1)  sinn(x)dx - I sinn(x)dx - I , , |
|
so
I = 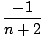 sinn+1(x)cos(x) + sinn+1(x)cos(x) +   sinn(x)dx sinn(x)dx |
|