Problem :
Give an example of a series that converges but does not converge absolutely.
Consider the series
Convergence follows from the alternating series test, whereas absolute convergence
fails because the harmonic series diverges.
Problem :
Prove that  (- 1)ne-n2 converges.
(- 1)ne-n2 converges.
The result follows from the alternating series test by noting that
e-(n+1)2≤e-n2 and that
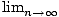 e-n2 = 0
e-n2 = 0.
Problem :
Determine whether or not
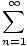 (- 1)n (- 1)n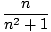 |
|
converges.
The series converges by the alternating series test, since the absolute value of
the
n-th term in the series is
Notice that the convergence is not absolute.