Problem :
Compute the Taylor series for f (x) = 1/(1 + x).
The first few derivatives of the function are
so
f (0) = 1,
f'(0) = - 1,
f''(0) = 2,
f(3)(0) = - 6. The general
case is clearly that
f(n)(0) = (- 1)nn!. Hence the Taylor series
for
f (x) is
| p∞(x) | = | 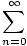  xn xn |
|
| | = | 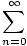 (- 1)nxn (- 1)nxn |
|
| | = | 1 - x + x2 - x3 + ... |
|
Problem :
What is the Taylor series of a polynomial p(x) = anxn + an-1xn-1 + ... + a0?
It is easy to check that the Taylor series of a polynomial is the polynomial itself!
(All the coefficients of higher order terms are equal to
0.)