Problem :
Approximate e0.1 to within 10-3 using Taylor's formula.
The error term in Taylor's formula is
where
c is some number in the interval
(0, 0.1). Thus
r3(0.1) < 1/3000 < 10-3,
so it is sufficient to go up to the degree
2 term in approximating
e0.1. We have
e0.1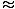 1 + 0.1 + 1 + 0.1 + 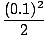 = 1.105 = 1.105 |
|
Problem :
Approximate sin(- 0.1) to within 10-5. The Taylor series for sin(x) begins
The absolute value of the error term in Taylor's formula is
Noting that
| r4(- 0.1)|≤| 0.1|4/4!≤10-5, we see that we need to use up to the
degree
4 term in the Taylor series. We have
sin(- 0.1) 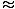 (- 0.1) - (- 0.1) - 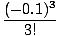 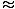 –0.09983 –0.09983 |
|