Problem :
Compute the Taylor polynomial at 0 of degree 3 for f (x) = sin(ex).
The first few derivatives are
| f'(x) | = | cos(ex)ex |
|
| f''(x) | = | cos(ex)ex - sin(ex)e2x |
|
| f'''(x) | = | f''(x) - [sin(ex)2e2x + cos(ex)e3x] |
|
Substituting
0 for
x yields
f (0) = sin(1),
f'(0) = cos(1),
f''(0) = cos(1) - sin(1),
f'''(0) = - 3 sin(1), so the desired Taylor polynomial is:
sin(1) + cos(1)x + 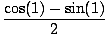 + + 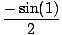 x3 x3 |
|
Problem :
Approximate log(0.8) using the Taylor polynomial of degree 3 at x = 1 for
log(x).
The desired Taylor polynomial is
(x - 1) - 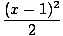 + +  |
|
Substituting
0.8 for
x, we have
log(0.8)  -0.222
-0.222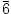
.
Problem :
Find the Taylor series for sin(x) + cos(x).
Adding term-by-term, we have