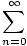Previous Next

x2n+1    

This series has infinite radius of convergence. Noting that | f(n)(x)|≤1 for all n≥ 0 (since f(n)(x) is equal to sin(x), cos(x), -sin(x), or -cos(x)), we get a bound on the remainder term:

| rn(x)| = xn≤| x|n    

Since 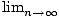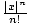= 0 for all real numbers x, we have 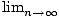| rn(x)| = 0, so the Taylor series for f (x) = sin(x) converges to f (x) for all x.

The situation with g(x) = cos(x) is similar. The first few derivatives at 0 are


g(0) = 1  
g'(0) = 0  
g(2)(0) = - 1  
g(3)(0) = 0  
g(4)(0) = 1  

so the Taylor series at 0 looks like

1 - + - + ... = x2n    

Again the radius of convergence is infinite, and the same estimate applies to the remainder term as for the sine function, so cos(x) coincides with the function represented by its Taylor series for all x.

The Exponential Function

The exponential function has perhaps the simplest Taylor series of all. If f (x) = ex, then f(n)(x) = ex for all n≥ 0, so the Taylor series for f at 0 is just

Previous page Some Common Taylor Series page 1 Next page Some Common Taylor Series page 3

Take a Study Break