Special names are given to geometric figures that lie on or inside circles. Among these geometric figures are arcs, chords, sectors, and segments.
Arc
The arc of a circle consists of two points on the circle and all of the points on the circle that lie between those two points. It's like a segment that was wrapped partway around a circle. An arc is measured not by its length (although it can be, of course) but most often by the measure of the angle whose vertex is the center of the circle and whose rays intercept the endpoints of the arc. Hence an arc can be anywhere from 0 to 360 degrees. Below an arc is pictured.
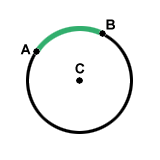
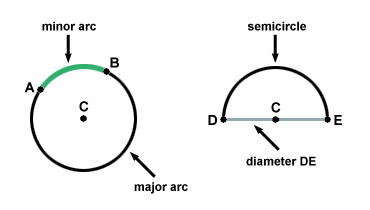
The arc above contains points A, B, and all the points between them. But what if the arc went the other way around the circle? This brings up an important point. Every pair of endpoints defines two arcs. An arc whose measure is less than 180 degrees is called a minor arc. An arc whose measure is greater than 180 degrees is called a major arc. An arc whose measure equals 180 degrees is called a semicircle, since it divides the circle in two. Every pair of endpoints on a circle either defines one minor arc and one major arc, or two semicircles. Only when the endpoints are endpoints of a diameter is the circle divided into semicircles. From this point on, unless otherwise mentioned, when arcs are discussed you may assume the arc is a minor arc.
A central angle is an angle whose vertex is the center of a circle. Any central angle intercepts the circle at two points, thus defining an arc. The measure of a central angle and the arc it defines are congruent.
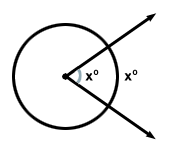
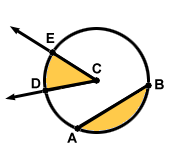
Chord
A chord is a segment whose endpoints are on a circle. Thus, a diameter is a special chord that includes the center.
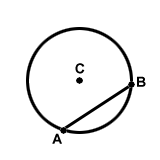
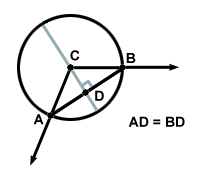
Chords have a number of interesting properties. Every chord defines an arc whose endpoints are the same as those of the chord. For example, a diameter and semicircle are a chord and arc that share the same endpoints. The union of a chord with a central angle forms a triangle whose sides are the chord and the two radii that lie in the rays that make up the angle. This kind of triangle is always an isosceles triangle--we'll define that term in Geometry 2. Also, the diameter perpendicular to a given chord (remember, there is only one such diameter because a diameter must contain the center) is also the perpendicular bisector of that chord. These ideas are illustrated below.
Sectors and Segments
Central angles and chords also define certain regions within a circle. These
regions are called sectors and segments. A sector of a circle is the
region enclosed by the central angle of a circle and the circle itself. A
segment of a circle is the region enclosed by a chord and the arc that the chord
defines. A given segment is always a subregion of the sector defined by the
central angle that intersects the circle at the endpoints of the chord
that defines the given segment. Sound a little complicated? It isn't. Take a
look at the drawing.