Previous Next

In this text we'll just introduce a few simple techniques for evaluating limits and show you some examples. The more formal ways of finding limits will be left for calculus.

A limit of a function at a certain x-value does not depend on the value of the function for that x. So one technique for evaluating a limit is evaluating a function for many x-values very close to the desired x. For example, f (x) = 3x. What is f (x)? Let's find the values of f at some x-values near 4. f (3.99) = 11.97, f (3.9999) = 11.9997, f (4.01) = 12.03, andf (4.0001) = 12.0003. From this, it is safe to say that as x approaches 4, f (x) approaches 12. That is to say, f (x) = 12.

The technique of evaluating a function for many values of x near the desired value is rather tedious. For certain functions, a much easier technique works: direct substitution. In the problem above, we could have simply evaluated f (4) = 12, and had our limit with one calculation. Because a limit at a given value of x does not depend on the value of the function at that x-value, direct substitution is a shortcut that does not always work. Often a function is undefined at the desired x-value, and in some functions, the value of f (a)≠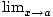f (x). So direct substitution is a technique that should be tried with most functions (because it is so quick and easy to do) but always double-checked. It tends to work for the limits of polynomials and trigonometric functions, but is less reliable for functions which are undefined at certain values of x.

The other simple technique for finding a limit involves direct substitution, but requires more creativity. If direct substitution is attempted, but the function is undefined for the given value of x, algebraic techniques for simplifying a function may be used to findan expression of the function for which the value of the function at the desired x is defined. Then direct substitution can be used to find the limit. Such algebraic techniques include factoring and rationalizing the denominator, to name a few. However a function is manipulated so that direct substitution may work, the answer still should be checked by either looking at the graph of the function or evaluating the function for x- values near the desired value. Now we'll look at a few examples of limits.

What is ?

Figure %: f (x) =
By direct substitution and verification from the graph, = - .

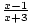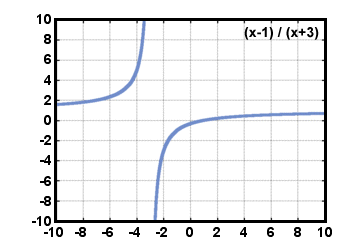
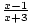
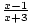What is ?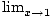

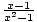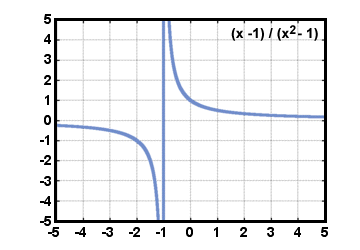
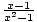
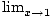
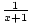Figure %: f (x) =
Direct substitution doesn't work, because f is undefined at x = 1. By facotring the denominator into (x + 1)(x - 1), though, the (x - 1) term cancels on the top and bottom, and we are left evaluating . By direct substitution, the limit is .

Consider the function f (x) = xforx < 0, f (x) = x + 1forx≥ 0. What is 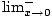f (x), what is 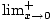f (x), and what is f (x)?

Figure %: f (x) = x for x < 0, f (x) = x + 1 for x≥ 0
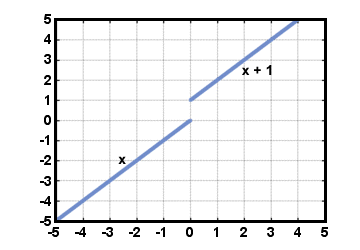
The one-sided limit from the left is 0. This we can tell both from direct substitution and by studying the graph. Using the same techniques, we find the one-sided limit from the right is 1. By the rules of the nonexistent limit, f (x) does not exist, because is 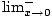f (x)≠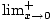f (x).

Consider the function f (x) = xforallx≠3, f (x) = 2forx = 3. What is 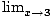f (x)?

Figure %: f (x) = x for all x≠3, f (x) = 2 for x = 3
Direct substitution gives the limit at 2, but more careful inspection of the graph and the values surrounding x = 3 show that in fact the limit of f at x = 3 is 3. This is a prime example of how the value of a function at x has no impact on the limit of that function at x.

Previous section Next section

Take a Study Break