Carbon Dating
Carbon dating is a technique used by scientists to date fossils. It relies on
the principle that the C14 isotope of carbon decays (this is called
radioactive decay) into another isotope of carbon, C12 at a rate
proportional to its mass. This means that it has a constant relative rate of
decay. The same equation is used for this situation as for continuous
compounding and population growth. With situations involving decay, the rate of
growth is always negative.
The half-life of a substance is the amount of time it takes for half of that
substance to decay. It is only a property of substances that decay at a rate
proportional to their mass. Through research, scientists have agreed that the
half-life of C14 is approximately 5700 years. The decay constant, k, for
carbon-14 can be calculated using the half-life. Using the constant relative
rate of decay function, we say that the remaining amount of carbon-14 C(t) = C(0)e-kt. k is negative because C(t) decreases as t increases.
half-life
C(5700) = C(0)e-5700k = 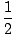 C(0) C(0) |
|
e-5700k = 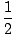 |
|
ln e-5700k = ln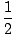 |
|
-5700k = ln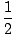 |
|
- k = 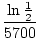 |
|
With a little manipulation, the function
C(t) = C(0)e-kt can now be
simplified to
C(t) = C(0)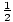

. Then, given the
estimated percentage of the original amount of
C14 left in an organism, its
age can be approximated.