Previous Next

An arithmetic sequence is a sequence in which the difference between each consecutive term is constant. An arithmetic sequence can be defined by an explicit formula in which an = d (n - 1) + c, where d is the common difference between consecutive terms, and c = a1. An arithmetic sequence can also be defined recursively by the formulas a1 = c, an+1 = an + d, in which d is again the common difference between consecutive terms, and c is a constant.

The sum of an infinite arithmetic sequence is either ∞, if d > 0, or - ∞, if d < 0.

There are two ways to find the sum of a finite arithmetic sequence. To use the first method, you must know the value of the first term a1 and the value of the last term an. Then, the sum of the first n terms of the arithmetic sequence is Sn = n(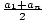). To use the second method, you must know the value of the first term a1 and the common difference d. Then, the sum of the first n terms of an arithmetic sequence is Sn = na1 + (dn - d ).

Previous section Next section

Take a Study Break