Previous

Problem : Solve the following equation: cos(x) - tan2(x) = 1.

Using the identity 1 + tan2(x) = sec2(x), the equation cos3(x) = 1 results. Therefore cos(x) = 1, and x = 0.

Problem : Solve the following equation: 2 sec(x)sin3(x) = cos(x)tan2(x).

Resolving everything into sines and cosines and then cancelling, we have sin(x) = 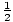. x = ,.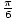

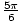
Problem : Calculate cos(15) using the fact that cos(30) = .

cos(15) = = .9659.

Problem : θ is in the first quadrant, and tan(θ) = 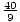. Find the sine, cosine, and tangent of 2θ.

sin(θ) = 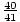. cos(θ) = 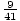. With these values, we can calculate sine, cosine, and tangent of 2θ. sin(2θ) = 2 sin(θ)cos(θ) 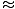0.4283.cos(2θ) = cos2(θ) - sin2(θ) 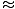-0.9036.tan(2θ) =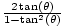 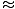- 0.4740.

Problem : Express the following as a function of a single angle: .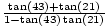

tan(64).

Problem : Express the following as a sum or difference: cos(100)cos(50).

cos(100)cos(50) = 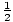(cos(100 + 50) + cos(100 - 50)) = 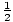(cos(150) + cos(50).

Problem : Simplify: sin2(x) + cos2(x) - sec2(x) + tan2(x).

sin2(x) + cos2(x) - sec2(x) + tan2(x) = 0.

Problem : Solve: cos(x)tan(x) = csc2(x) - cot2(x) - 1.

x = {0,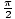, Π,}
Previous section

Take a Study Break