Previous Next

Escape Velocity

If a projectile is blasted from the earth, it may do one of several things. Most projectiles have a speed such that they soon begin to curve back down towards the earth--this is the parabolic flight described by projectile motion. However it is possible to give a projectile sufficient speed (which is directly proportional to its energy) such that its downward curvature is exactly matched by the curvature of the earth. In this case, the projectile will never reach the ground, and will in fact be in a circular orbit around the earth. If the projectile is launched with even greater energy, it will describe an elliptical path. This is consistent with what we have just seen in Solving the Orbits, where elliptical orbits were seen to have higher energies than circular ones. In fact, because ε = , the greater the eccentricity of the orbit, the greater the energy. shows the differing paths of projectiles with increasing energy.

Figure %: Trajectories of orbits with different energies.

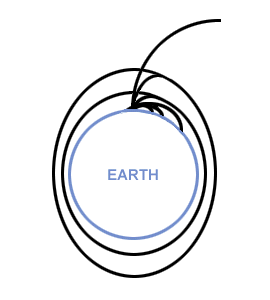
However, when the projectile is launched with even greater velocity, it will have a sufficient energy to escape the gravitational field of the earth (or any planet or star). In these cases, a parabolic or hyperbolic orbit results. We also saw there that for a parabolic orbit the projectile has barely enough energy to reach infinity--that is, it arrives at infinity with no kinetic energy. Thus, the energy for a parabolic orbit is the minimum amount of energy we can give to a projectile such that it will escape from the gravitational field in which it is caught.

Let us now calculate the velocity corresponding to this parabolic energy. This is the surface velocity required to completely escape the gravitational field of a planet. We saw in Solving the Orbits that this corresponds to zero total energy. That fact makes sense, because energy is conserved and the projectile must have zero energy at infinity. Thus we can write an expression for the total energy equal to kinetic plus potential:

E = 1/2mv2 - = 0    

Solving this for v we find:

v =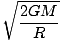    

Where M and R are the mass and radius of the gravitating body. Note that this value is independent of the mass of the projectile.

Viscous Drag

Another interesting orbital phenomenon results when low-earth satellites experience viscous drag (friction) due to the atmosphere. We would expect that the drag due to the atmosphere would slow the satellite down. It is observed that eventually the satellites spiral back towards the earth and burn up in the atmosphere (the atmosphere gets denser as the satellites approach the earth, and thus heat due to friction increases). The force on a satellite in orbit can be given by both the Universal Law of Gravitation and the expression for centripetal force. Hence we can write:

= âá’v =    

However, this equation implies that as the velocity of the satellite decreases, the orbit should increase in radius. This appears to contradict our idea that viscous drag slows the satellite down, causing it to spiral towards the earth. We would expect viscous drag to cause the satellite to spiral away from the earth. In fact, the equation is right, and our intuition about the effect of the drag was wrong. The viscous drag due to the atmosphere actually speeds up the satellite in its orbit, but causes it to move to a lower energy (lower radius) orbit. In this lower orbit, the potential energy of the satellite is reduced, but since it has increased in speed, the kinetic energy has increased. Only in this way can the total energy be conserved.

Previous section Next section

Take a Study Break