Position for an object is given by
s(t) = 2t2 - 6t - 4, measured in feet with time in seconds
Problem :
What is the average velocity of the object on [1, 4]?
| vavg | = | 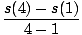 = = 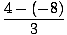 |
|
| | = | 4 feet per second |
|
Problem :
What is the instantaneous velocity at t = 1 and at t = 4?
v(t) = s'(t) = 4t - 6
v(1) = - 2 feet per second
v(4) = 10 feet per second
Thus, the particle changes direction during this time interval.
Problem :
What is the total distance traveled on [1, 4]?
It would not be correct to simply take
s(4) - s(1) (the net change in position) in this case
because the object spends part of the time moving forward, and part of the time moving
backwards. When the object doubles back on itself, that overlapping distance is not
captured by the net change in position.
To solve this problem, we must add up the distances that the object travels when it is
moving in one direction. To do this, we must find the point at which it changes direction.
This occurs when the instantaneous velocity is equal to zero.
v(t) = 4t - 6
v(t) = 0 at
x = 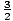
So, the object moves backward on
(1,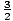 )
) and forwards on
(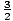 , 4)
, 4).
The distance traveled on the first interval is
 s(
s(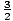 ) - s(1)
) - s(1)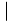 =
= 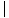 -3 - (- 6)
-3 - (- 6)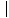 = 3 feet
.
= 3 feet
.
The distance traveled on the second interval is
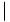 s(4)-s(
s(4)-s(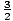 )
) =
= 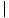 10-(-3)
10-(-3) = 13 feet
.
= 13 feet
.
The total distance traveled is the sum of these two, which is 16 feet.
Problem :
A ball is dropped vertically from a height of 100 meters. Assume that the acceleration
due to gravity has a magnitude of 10 m/s2.
What is the velocity at t = 2?
Here, acceleration is in the negative direction, since it is toward the ground, which is
designated with a coordinate of zero.
So,
a = - 10 meters per second per second, and
v(t) = v0 + a(t). But the initial velocity is zero, so
v(t) = - 10t.
v(2) = - 20 meters per second.
Problem :
What is the position of the ball at t = 2?
s0 = 100, so
s(t) = 100 + 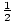 (- 10)t2
s(t) = 100 - 5t2
s(2) = 100 - 20
s(2) = 80
(- 10)t2
s(t) = 100 - 5t2
s(2) = 100 - 20
s(2) = 80 meters from the ground