Previous Next

Average Rates of Change

Suppose s(t) = 2t3 represents the position of a race car along a straight track, measured in feet from the starting line at time t seconds. What is the average rate of change of s(t) from t = 2 to t = 3?

The average rate of change is equal to the total change in position divided by the total change in time:


Avg Rate =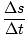  
  =  
  =  
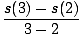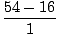  = 38 ft per second  

In physics, velocity is the rate of change of position. Thus, 38 feet per second is the average velocity of the car between times t = 2 and t = 3.

Instantaneous Rates of Change

What is the instantaneous rate of change of the same race car at time t = 2?

The instantaneous rate of change measures the rate of change, or slope, of a curve at a certain instant. Thus, the instantaneous rate of change is given by the derivative. In this case, the instantaneous rate is s'(2).


s'(t)=6t2  
s'(2)=6(2)2 = 24 feet per second  

Thus, the derivative shows that the racecar had an instantaneous velocity of 24 feet per second at time t = 2.

Previous section Next page Rates of Change and Applications to Motion page 2

Take a Study Break