Intuition can usually lead to the right answer with these problems, but the following is a
more methodical way of calculating limits at infinity.
Evaluating Limits at Infinity
In order to find horizontal asymptotes, we must evaluate limits as x approaches
infinity. To evaluate the limits of rational functions at infinity, first divide each of the terms in the
numerator and the denominator by the highest. For example, to evaluate
first divide each of the terms in the numerator and denominator by the highest
power of x present in the function. In this case, that is x3.
then evaluate the individual limits using the following rule: if r is a rational number greater than zero such that
xr is defined for all x, then
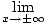 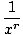 = 0 = 0 |
|
Applying this rule in this case leads to the following: