The Lorentz Transformations
Michelson and Morley's experiments (see the
Introduction to this
topic) showed that there was no difference
in the speed of light when the earth was moving through the ether in different directions, suggesting
that there was no such thing as an ether. However, the properties of the ether underpinned much
of physics and, understandably, physicists were not willing to give it up easily. In the 1890s, G.F.
Fitzgerald and H.A. Lorentz independently proposed that any length (including Michelson and Morley's
experimental apparatus) must shrink in the direction of motion through the ether by a factor 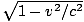 =
= 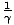 . In fact, Fitzgerald and Lorentz saw that for the laws of physics to be
preserved in all inertial reference frames, the Galilean transformations of Newtonian physics had to
be replaced. However, no rationale or theory was provided for these particular
transformations; Fitzgerald and Lorentz deduced their transformations from the mathematics of
electromagnetism and not from any understanding of the relativistic nature of motion. It was not until 1905 that
Einstein's theory showed the rationale behind the Lorentz transformations (sometimes called
the Lorentz-Fitzgerald transformations).
. In fact, Fitzgerald and Lorentz saw that for the laws of physics to be
preserved in all inertial reference frames, the Galilean transformations of Newtonian physics had to
be replaced. However, no rationale or theory was provided for these particular
transformations; Fitzgerald and Lorentz deduced their transformations from the mathematics of
electromagnetism and not from any understanding of the relativistic nature of motion. It was not until 1905 that
Einstein's theory showed the rationale behind the Lorentz transformations (sometimes called
the Lorentz-Fitzgerald transformations).
It is possible to derive the lorentz transformations from the postulates of Special Relativity). However, the derivation is long and not particularly enlightening because there are several assumptions which are hard to justify without delving deeply into the mathematics of spacetime. The result of the derivation is:
| Δx = γ(Δx' + vΔt) | |||
| Δt = γ(Δt' + vΔx/c2) |
where:
γâÉá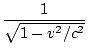 |
What does all this mean? The primed variables (x' and t') refer to a coordinate system, call it F', that is moving with speed v with respect to another frame F (the unprimed variables, x and t, refer to F). Further, F and F' have their x-axes pointing in the same direction and the velocity of F' is entirely in the x-direction. makes this clearer:
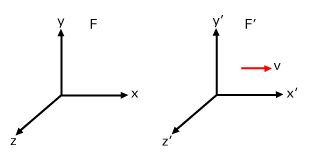
| Δx' = γ(Δx - vΔt)Δt' = γ(t - vx/c2) |
Also, the Lorentz transformation in the y and z-directions are just Δy = Δy' and Δz = Δz'.
Note that in the limit v < < c (that is, when the velocity involved is nowhere near the speed of light),
γ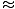 1 and the transformations reduce to x = x' + vt' and t = t'. As we would expect
(from the correspondence principle), these are the familiar Galilean transformations. We will now
see how the lorentz transformations can be easily applied to show the results we have already derived.
1 and the transformations reduce to x = x' + vt' and t = t'. As we would expect
(from the correspondence principle), these are the familiar Galilean transformations. We will now
see how the lorentz transformations can be easily applied to show the results we have already derived.
Lorentz and Simultaneity
If two events are simultaneous in F', then Δx' = x' and Δt' = 0. Plugging into the equation
for Δt we find: Δt = 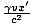 , which is non-zero unless x' = 0 or v = 0.
Thus the events do not occur simultaneously in frame F (Deltat
, which is non-zero unless x' = 0 or v = 0.
Thus the events do not occur simultaneously in frame F (Deltat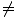 0 implies that there is a time
difference between the events).
0 implies that there is a time
difference between the events).
Lorentz and Time Dilation
If two events occur at the same place in F' then Δx' = 0 and Δt' = t'. Using the second equation, the separation in time between the events in F is: Δt = γΔt' (for Δx' = 0). Similarly if events occur in the same place in F, Δx = 0 and Δt = t. Then the second inverse transformation tells us: Δt' = γΔt (for Δx = 0). Thus we again have arrived at the seeming-contradiction we saw in Section 2. However, here it is clear that one equation applies when Δx = 0 and one when Δx' = 0; the nature of the Lorentz transformations themselves assure us that these cannot both the satisfied for any two events.
Lorentz and Length Contraction
In the section on length contraction we noted that any measurement of length requires that the coordinates of the ends of the object be recorded simultaneously. To measure the length of a moving train, for example when might place two time bombs, primed to go off simultaneously, at opposite ends of the train. The length of the train is the distance between the explosions. Note that if the explosions were not simultaneous (say the explosion at the rear occurred first), the train would move between the explosions and you would measure an incorrect length (too long, in this case). Thus if we have a pole of length l' in frame F' and it is lying along the x'-axis, what is the length in F? In F we make our simultaneous measurements and we have Δx = x and Δt = 0. From the first Lorentz transformation we have: Δx' = γΔx (for Δt = 0). Δx is by definition the length in F, and since the pole is not moving in F', Δx' is its length in F'. Thus l = l'/γ, just as we discovered in Section 2. We could also analyze a situation when a pole is at rest in F, and find the seeming-contradictory result l' = l /γ. As we have seen the former equation applies only to situations where Δt = 0 and the latter to those where Δt' = 0. Everything depends on which frame the simultaneous measurements are made. (See Section 2.)













