Please wait while we process your payment
If you don't see it, please check your spam folder. Sometimes it can end up there.
If you don't see it, please check your spam folder. Sometimes it can end up there.
Please wait while we process your payment
Get instant, ad-free access to our grade-boosting study tools with a 7-day free trial!
Learn more



This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!

Annual
2-49 accounts
$22.49/year + tax
50-99 accounts
$20.99/year + tax
Select Quantity
Price per seat
$29.99 $--.--
Subtotal
$-.--
Want 100 or more? Request a customized plan
You could save over 50%
by choosing an Annual Plan!

SAVE OVER 50%
compared to the monthly price!
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
$22.49/month + tax
Save 25%
on 2-49 accounts
$20.99/month + tax
Save 30%
on 50-99 accounts
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!
You will only be charged after the completion of the 7-day free trial.
If you cancel your account before the free trial is over, you will not be charged.
You will only be charged after the completion of the 7-day free trial. If you cancel your account before the free trial is over, you will not be charged.
Order Summary
Annual
7-day Free Trial
SparkNotes PLUS
$29.99 / year
Annual
Quantity
51
PLUS Group Discount
$29.99 $29.99 / seat
Tax
$0.00
SPARK25
-$1.25
25% Off
Total billed on Nov 7, 2024 after 7-day free trail
$29.99
Total billed
$0.00
Due Today
$0.00
Promo code
This is not a valid promo code
Card Details
By placing your order you agree to our terms of service and privacy policy.
By saving your payment information you allow SparkNotes to charge you for future payments in accordance with their terms.
Powered by stripe
Legal
Google pay.......



Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Your PLUS subscription has expired
Please wait while we process your payment
Please wait while we process your payment

Determining the Rate Law

To calculate the order of the reaction for bromine, notice that experiments 1 and 2 hold the concentration of acetone constant while doubling the concentration of bromine. The initial rate of the reaction is unaffected by the increase in bromine concentration, so the reaction is zero order in bromine. We can prove this mathematically by taking the ratio of the rates from experiments 1 and two:
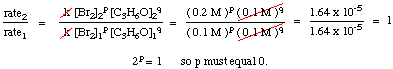
As you can see in the above equations, by holding the concentrations of all but one species constant between two experiments, you can calculate the order of the reaction in a single reactant at a time. By similar reasoning, we can conclude that because the rate of reaction doubled when the concentration of acetone was doubled (cf. experiments 1 and 3) the reaction must be first order in acetone. However, had the rate quadrupled or octupled with a doubling of the acetone concentration, the reaction would have been second or third order in acetone, respectively. In practice, you will likely never see a reaction with an order higher than 3. If you calculate an order higher than 3 for a reaction, double check your math because that is highly unusual. If you compute a fractional power for a reactant's order, do not be discouraged; they are quite common (especially half-order reactions).
To calculate the value of k, the rate constant, you simply plug into the rate law the values of the concentrations, the orders, and the rate of the reaction from any one of the three experiments. All three experiments should give a value of 1.64 x 10-4 s-1. You should prove this to yourself.
One major disadvantage to using the method of initial rates is the need to perform multiple experiments. Another disadvantage is that it works only for relatively slow reactions. If your reaction proceeds too fast, the rate that you measure will have a large range of uncertainty. To combat these problems, chemists have developed a method that uses data on concentration versus time during a reaction to infer the order of a reaction. The strategy works by comparing concentration versus time information to the mathematical predictions made by integrated rate laws. This is usually accomplished by assuming that a reaction has a certain order and making a plot out of the data that should be linear if the assumption about the rate law is correct. If we guess correctly, the graph is linear. If we are wrong, then the graph is curved and we need to choose another order against which to plot our data.
To practice this method, we will first need to know the forms of the integrated rate laws for some common reaction orders. Luckily, only orders zero through two are common so we need to only consider reactions with these three orders. Due to the mathematical complexities of the problem, we will only consider rate laws of the form rate = [A]n. However, with some experimental tricks I will explain below, that treatment does allow us to use the method of integrated rates for a reaction with any arbitrary rate law.
By integrating the differential rate law (the simple rate law from Heading ), we derive the integrated rate law for a reaction. Without proof, we present below the forms of the integrated rate laws for reaction orders zero through two:
Please wait while we process your payment





