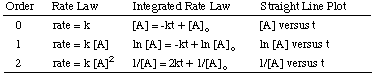
As you can see, each order of reaction has a unique input and output variable that produces a straight line. For example, if we graph the following rate data for the decomposition of H2O2 assuming that it could be zero, first, or second order, we find that only the graph for a 2nd order reaction (1/[A] versus t) gives a straight line. Therefore, the reaction has the rate law rate = k [H2O2]2.

Assuming that we did not know that the decomposition is second order, we will make a series of three graphs to determine the order of the reaction:
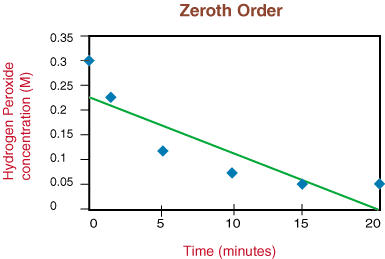
If the graph was linear, we would conclude that the rate law is zero Order, but it is not. Therefore, let's see if it is first order by plotting ln [H2O2] versus time in the following graph:
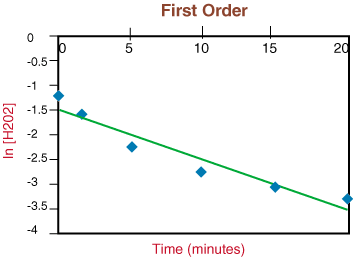
Seeing that the reaction is not first order due to the non-linearity of the above graph, we move to plotting 1/[H2O2] versus time to test whether the decomposition reaction is second order.
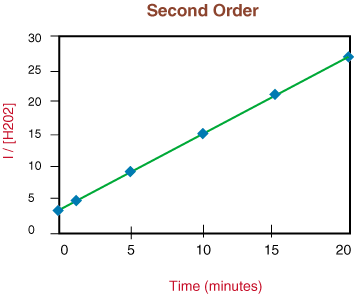
Because the above graph is linear, we know that the reaction is second order. The slope of the line is twice the rate constant, k from the rate law.
What you should learn from the above discussion is that you can use integrated rate laws to determine both the rate constant for a reaction and the form of the rate law. It may seem more complicated to use integrated rate laws rather than the method of initial rates to determine the rate law, but it really does take much longer to perform and analyze the several reactions needed for the method of initial rates than it does to produce the necessary graphs for the integrated rate law method--especially with a good graphing program.
You may have noticed that we only list three integrated rate laws, ignoring rate laws like rate = k [A] [B]. That doesn't mean we can't use integrated rate laws to determine the rate law for those types of reactions. We simply must be more clever about how we do it. For a two- component second order reaction with a rate law rate = k [A] [B], we can make the concentration of B so large as compared to A that the concentration of B is almost constant. Assuming that the concentration of B is constant, the reaction becomes pseudo-first order--that is, the reaction will behave as if it was first order. The kinetics data for this reaction will give a graph of ln [A] versus time that is linear, telling us that the reaction is first order in A. If the reaction happened to be second order in A, in the present example, then a graph of 1/[A] versus time would be linear. We can, similarly, determine the order of B by making the concentration of A large. For multiple component rate laws, you can simply make the concentration of all reagents but the one of interest large to iteratively determine the order of the reaction in each component. (Chemists are fond of using the word 'iterative' to say 'repetitive'.)
Half-Lives
An earlier and less common way to measure rate is by the half-life of a reaction. A half-life is the time it takes for one half of the starting material to be transformed into its products. Often you will hear half-life associated with radioactive decay phenomena (which follow first order kinetics), but the term can be applied to any reaction.
The half-life of a reaction not only depends on the rate constant of the reaction (those with larger k's have shorter half-lives) but also on the integrated rate law for the reaction. To derive the form of the half-life expression for a first order reaction, we start with its integrated rate law, and then substitute the value 0.5 for the ratio of [A] to [A]o:
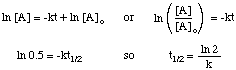
Using the same techniques with the different integrated rate laws, you can derive the half-life expression for a reaction of any order. Summarized below are the half-lives for reactions of orders zero through two.
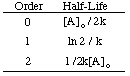


 payment page
payment page



