We end this chapter with a quick look at price discrimination. Sometimes, firms with at least some market power are able to increase their profits by offering the same good at two or more different price points, to different segments of buyers. For example, a movie theater near a college may sell movie tickets at $16 but offer them at $10 to anyone who can show proof of student status. The idea is to attract buyers who (for the most part) would not pay $16, without dropping the price to $10 for everyone.
Because the theater has market power (let’s suppose it is the only theater near the college), the demand curve for the theater’s product slopes downward. The marginal revenue (MR) curve does the same. To keep things simple, suppose that the marginal cost (MC) curve is flat at $3. (Every moviegoer costs the theater $3 to greet and to clean up after.) The single price that would maximize profit, according to the MR = MC rule, is $13:
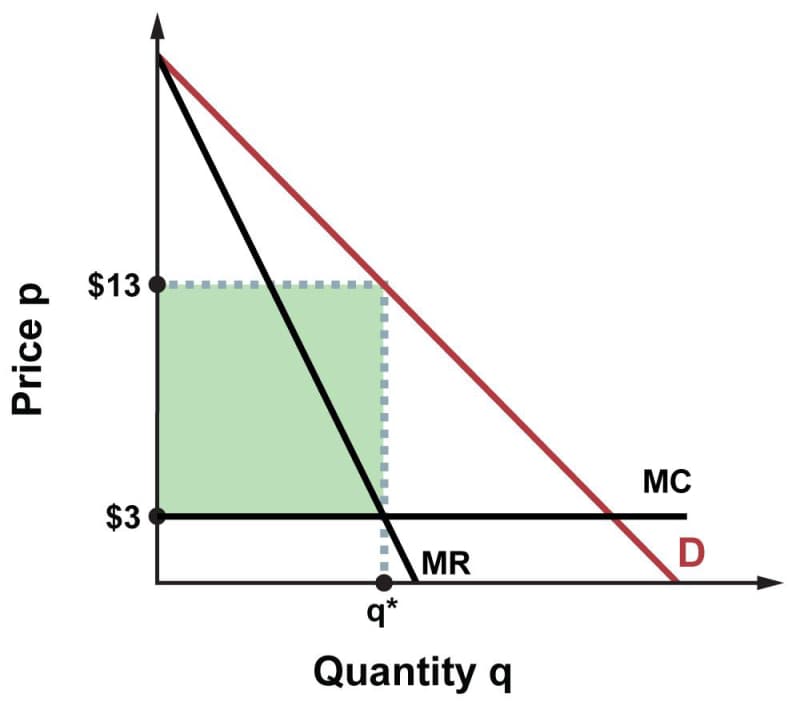
The green rectangle represents the theater’s profit: $10 per ticket (ticket price minus theater’s cost) times the number of tickets sold.
But now suppose that non-students are all willing to pay $16 or more. Then they represent the left end of the demand curve. For a theater offering tickets to students at $10 and to non-students at $16, the area representing profit becomes significantly larger:
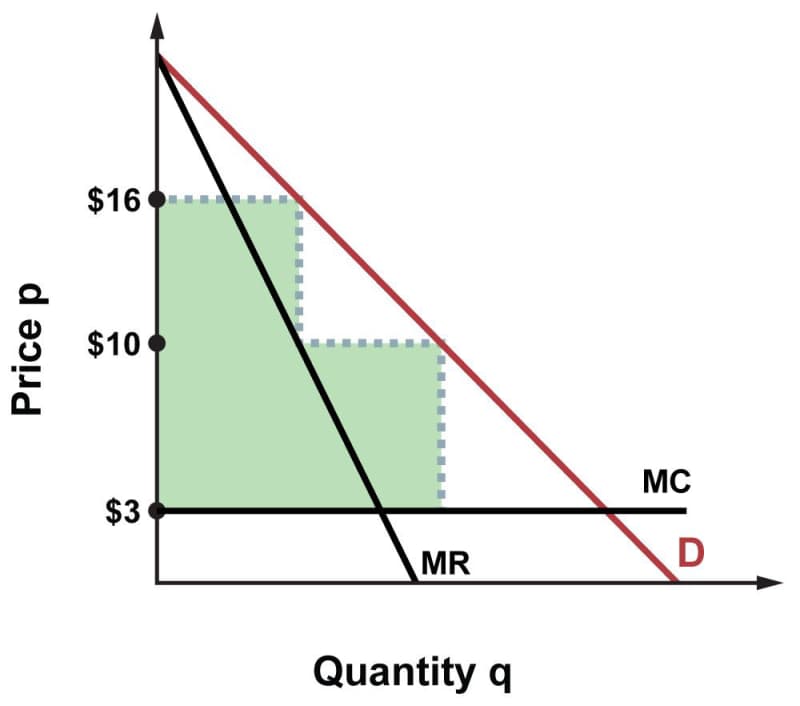
Not all firms with market power are able to engage in price discrimination. For one thing, there must be a practical means of segmenting the market into groups with different levels of willingness to pay, and charging each group a different price. But also, there must be a means of preventing resale. In the movie theater example, it would cause problems for the theater’s pricing scheme if students were to buy tickets at $10 and sell them to non-students at $14 or $15. Realistically, movie tickets are cheap enough that this isn’t likely to be a big problem, because a profit margin of $4 or $5 per ticket isn’t worth the work involved. But ticket resale (“scalping”) is an issue when the entertainment event in question is a championship football game or a pop music concert. Performers who try to sell discounted tickets to fan club members may encounter resellers posing as fans in order to obtain cheap tickets to resell at a higher price.













