More goods are preferred over fewer goods, but people don’t just get whatever they want. Their choices are limited to what they can afford. We normally represent this constraint as a line representing a consumer’s budget, draw on the same graph as the consumer's indifference curves. To draw a budget constraint, you need to know two things: 1) how much money the consumer has, and 2) the prices of the two goods being considered. Once you have both pieces of information, determine the maximum amount of the first good you can buy without buying any of the second, and the maximum amount of the second good you can buy without buying any of the first. Locate the corresponding points on the horizontal and vertical axes, and connect the points with a straight line.
To illustrate, suppose Tina has $100. She is deciding how many bottles of wine and how many wine glasses she wants to buy. If wine costs $20 a bottle and glasses cost $5 each, then she can buy at most \($100/$20 = 5\) bottles of wine, and she can buy at most \($100/$5 = 20\) wine glasses. Her budget constraint is then a line running from 20 on the glasses axis to 5 on the wine axis. If we know Tina’s indifference curves, we can draw her budget constraint in with them on the same graph.
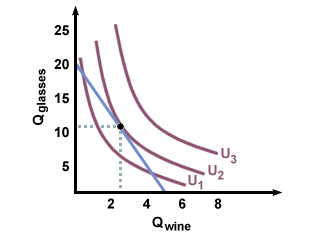
To maximize Tina’s utility, we find the outermost indifference curve that her budget constraint makes contact with. The point of contact indicates Tina’s optimal combination of wine and glasses. In this case, it is the second indifference curve that optimizes her utility given her budget. It looks like Tina will buy about 11 wine glasses and 2 bottles of wine. (Even though the optimal amount looks to be a little more than 2 bottles, she has to buy either 2 bottles or 3 bottles, and 2 is all she can afford. When doing such problems, never round up, since that will land you on combinations that are over budget.)













