Previous Next

In fact, when we multiply or divide both sides of an inequality by any negative number, the sign always flips. For instance, 4 > 2, so 4(- 3) < 2(- 3): -12 < - 6. -2 < 6, so 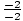> 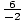: 1 > -3. This leads to the multiplication and division properties of inequalities for negative numbers.


Multiplication and Division Properties of Inequalities for positive numbers:

If a < b and c > 0, then ac < bc and <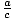
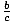
If a > b and c > 0, then ac > bc and >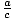
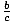
Multiplication and Division Properties of Inequalities for negative numbers:
If a < b and c < 0, then ac > bc and >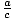
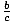
If a > b and c < 0, then ac < bc and <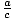

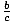
Note: All the above properties apply to ≤ and ≥.

Properties of Reciprocals

Note the following properties:

If a > 0, then 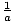> 0
If a < 0, then 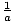< 0
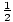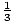
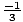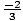
When we take the reciprocal of both sides of an equation, something interesting happens--if the numbers on both sides have the same sign, the inequality sign flips. For example, 2 < 3, but > . Similarly, > , but -3 < 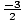. We can write this as a formal property:
If a > 0 and b > 0, or a < 0 and b < 0, and a < b, then >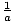
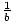
If a > 0 and b > 0, or a < 0 and b < 0, and a > b, then <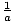


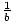
Note: All the above properties apply to ≤ and ≥.

Previous page Properties of Inequalities page 1 Next section

Take a Study Break