The Permutation Function
The permutation function is defined as:
P(n, k) = 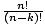
Examples:
| P(6, 3) | = | 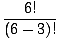 = = 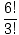 = = 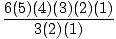 = 6(5)(4) = 120. = 6(5)(4) = 120. |
|
| P(9, 2) | = | 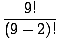 = = 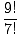 = = 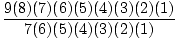 = 9(8) = 72. = 9(8) = 72. |
|
| P(7, 1) | = | 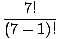 = = 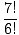 = 7 = 7 |
|
| P(10, 10) | = | 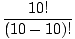 = = 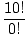 = = 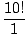 = 10! = 3628800. = 10! = 3628800. |
|
The permutation function yields the number of ways that n distinct items can
be arranged in k spots. For example, P(7, 3) = 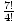 = 210. We can
see that this yields the number of ways 7 items can be arranged in 3 spots --
there are 7 possibilities for the first spot, 6 for the second, and 5 for the
third, for a total of 7(6)(5):
= 210. We can
see that this yields the number of ways 7 items can be arranged in 3 spots --
there are 7 possibilities for the first spot, 6 for the second, and 5 for the
third, for a total of 7(6)(5):
P(7, 3) = 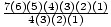 = 7(6)(5).
= 7(6)(5).
Example: The coach of a basketball team is picking among 11 players for
the 5 different positions in his starting lineup. How many different lineups
can he pick?
P(11, 5) = 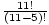 =
= 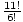 = 55440 different lineups.
= 55440 different lineups.
The Combination Function
The combination function is defined as:
C(n, k) = 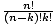
Examples:
| C(6, 3) | = | 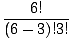 = = 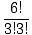 = 20. = 20. |
|
| C(9, 2) | = | 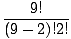 = = 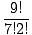 = 36. = 36. |
|
| C(7, 1) | = | 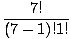 = = 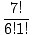 = 7. = 7. |
|
| C(10, 10) | = | 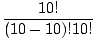 = = 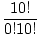 = 1. = 1. |
|