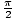Previous Next

In problems 1-3, for each of the following functions f defined on [a, b] find the c on [a, b] such that

f'(c) =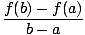    

Problem : 1) f (x) = x2 - 4x on [2, 4]


f'(c)= 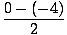= 2  
2c - 4=2  
c=3  

Problem : 2) f (x) = sin(x) + cos(x) on [0, 4Π]


  f'(c) = = 0  
  cos(x) - sin(x) = 0  
  x = ,,, or  

Problem : 3) f (x) = 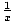on [1, 2]


f'(c) =  
  = -  
-  = -  
c = ±  

Problem : 4) On the interval [-5,5], there is no point at which the derivative of f (x) =|x| is equal to zero, even though f (- 5) = f (5). Is this a contradiction of Rolle's theorem?

No, it isn't a contradiction, since this function is not differentiable on the entire interval (- 5, 5).

Problem : Find the number c that satisfies Rolle's theorem for f (x) = sin(x) on the interval [0, Π].

(sin(x))' = cos(x)
cos(x) = 0 at x =
Previous section Next section

Take a Study Break