Motion With Constant Acceleration
This section refers to the special case of rectilinear motion in which the acceleration is
constant. In cases where the acceleration is constant, a(t) can be represented simply by
the constant a, and both velocity and position can be found by using the following
formulas:
| a(t) | = | a |
|
| v(t) | = | v0 + at |
|
| s(t) | = | s0 + v0t + 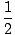 at2 at2 |
|
Where v0 is the initial velocity at time t = 0 and
s0 is the initial position at time t = 0. Note that these formulas
are in compliance with the relations v(t) = s'(t) and a(t) = v'(t).
A ball dropped vertically from a height travels in this fashion, because it is accelerated by
gravity at a constant rate of 9.8 meters per second per second.