Problem :
Apply the shell method to find the volume of the solid obtained by revolving the region
below the graph of f (x) = x2 from x = 0 to 1 about the y-axis (this solid looks
like a cylinder with a bowl carved out of the top).
The formula from the shell method gives
2Π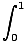 x(x2)dx x(x2)dx | = | 2Π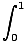 x3dx x3dx |
|
| | = | 2Π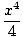 |01 |01 |
|
| | = | 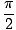 |
|
Problem :
Compute the volume of the square pyramid with base in the x = 0 plane with sides of
length 10 and vertex at the point (5, 0), using the cross-sectional area method.
The cross-section of the pyramid in the plane perpendicular to the
x-axis with a
particular
x-coordinate in the interval
[0, 5] is a square with sides of length
s(x) = 10 - 2x. Such a square has area equal to
A(x) = s(x)2 = (10 - 2x)2 = 4x2 - 40x + 100, so the
volume of the pyramid is given by
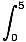 A(x)dx A(x)dx | = | 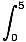 (4x2 - 40x + 100)dx (4x2 - 40x + 100)dx |
|
| | = |  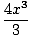 -20x2 + 100x -20x2 + 100x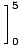 |
|
| | = |  |
|