payment page
-
Cross-Sectional Area Method
If A(x) is the cross-sectional area of a region perpendicular to a fixed axis at position x, defined between x = a and x = b, then the total volume of the region is
Vol =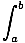 
A(x)dx
-
Disk Method
The volume of the region obtained by rotating the area under the graph of a function f (x) between x = a and x = b about the x-axis is equal to
Vol = 2Π 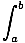f (x)2dx
This is an application of the cross-sectional area method, noting that that cross section to this surface of revolution perpendicular to the x-axis is a circle of radius f (x). -
Shell Method
The volume of the region obtained by rotating the area under a function f (x) between x = a and x = b about the y-axis is equal to:
Vol = 2Π 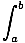xf (x)dx
-
Solid of Revolution
The solid swept out by a region in the plane when rotated about an axis. Examples include cylinders, cones, and spheres (all considered as solids with their interiors). The volume of such a region can be computed via the disk method or the shell method.
-
Surface of Revolution
The surface swept out by a curve in the plane when rotated about an axis. Examples include the surface of a cylinder, cone, or sphere, and more generally the surface of any solid of revolution.
