Problem :
Find the average value of f (x) = | sin(x)| from x = 0 to 2Π.
We compute
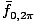 | = | 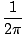 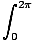 | sin(x)| dx | sin(x)| dx |
|
| | = | 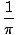 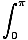 sin(x)dx sin(x)dx |
|
| | = | 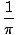 (- cos(x)|0Π) (- cos(x)|0Π) |
|
| | = | 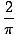 |
|
We could also have observed that in a
previous section
we found the
area under this function to be 4, which is by definition the product
of
2Π and the average value.
Problem :
What is the average y-coordinate of a point on the upper half of the unit circle centered
at the origin? (You may use that 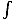
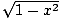 dx = (x/2)
dx = (x/2)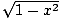 + (1/2)sin-1(x).)
+ (1/2)sin-1(x).)
The upper half of the unit circle centered at the origin is the graph of the function
f (x) = 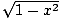
on the interval
[- 1, 1]. The average value of
f on this interval
equals
  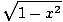 dx dx | | |
|
| | | =  (2) (2)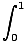 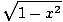 dx dx |
|
| | =   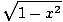 + +  sin-1(x)|01 sin-1(x)|01 | = 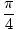 |
|
which is approximately equal to
0.79. Notice that this result
depends critically on the interpretation of the word "average". Here
we are thinking of average of the
y-coordinate as a function of
x.
If instead we considered the
y-coordinate as a function of arc
length around the circle, we would be asking for the average of
sin(t) on the interval
[0, Π], which is
2/Π.